Graf (teorija grafova)
Graf je skup bridova i čvorova koji opisuju odnose između objekata. Mogu biti usmjereni i neusmjereni te težinski i bestežinski. Koristi se za opisivanje relacija između dvaju objekata iz određene kolekcije. U ovom kontekstu odnosi se na neprazni skup vrhova i kolekciju bridova koji povezuju par vrhova.[1]
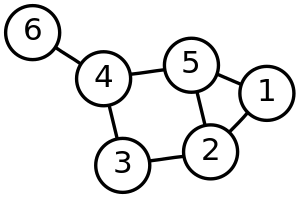
Definicija
urediDefiniran je dvama odvojenim skupovima i pripadajućim odnosima među njima. Ti skupovi su skup čvorova , skup grana, lukova dva su odvojena skupa.[2]
Matematički definirano, graf G predstavlja uređenu trojku G = (V(G), E(G), φG. Sastavni su joj dijelovi:
- neprazan skup V = V(G), čiji su elementi vrhovi od G
- skup E(G) disjunktan s V(G), čiji su elementi bridovi od G
- funkcija incidencije φG, koja svakom bridu od G pridružuje neuređen par (ne nužno različitih) vrhova od G.[2]
Kraći zapis koji se katkad primjenjuje za G = (V(G), E(G), φG jest [2]
U usmjerenom grafu neki su bridovi jednosmjerni. Ako u usmjerenom grafu možemo iz čvora A doći u čvor B ne znači da možemo iz čvora B doći u čvor A. Jednosmjernih bridova nema u neusmjerenim grafovima.
U težinskim grafovima svaki brid ima svoju vrijednost. U bestežinskim grafovima vrijednost svakog brida prema dogovoru iznosi 1.
Brid koji počinje i završava u istom vrhu zove se petlja. Ciklus je zatvorena staza u kojoj su svi unutarnji vrhovi međusobno različiti.[1] Drugim riječima, ciklus je staza koja počinje i završava u istome čvoru.
Povezan graf s n čvorova i n-1 bridova zove se stablo. U stablu nema ciklusa ni petlji.
Komponenta grafa je povezani dio grafa. U neusmjerenom grafu iz svakog čvora neke komponente možemo u svaki čvor te iste komponente. U nijednom grafu ne možemo preko bilo kojeg brida prijeći iz jedne komponente u drugu. Jedna komponenta može obuhvaćati i cijeli graf.
Čvor
urediČvor je osnovna gradivna jedinica grafa.
Za svaki čvor je poznat ulazni te izlazni stupanj. Ulazni stupanj označava broj bridova koji ulaze u taj čvor, a izlazni stupanj iznosi broj bridova koji izlaze iz čvora. U neusmjerenim grafovima, zbroj ulaznih stupnjeva svih čvorova jednak je zbroju izlaznih stupnjeva svih čvorova, a iznosi dvostruki broj bridova.
Stablo
urediStablo je povezan graf s n čvorova i n-1 bridova. U stablu postoji poseban čvor koji nazivamo korijen stabla.[3] U stablu nema ciklusa ni petlji.
Binarno stablo
urediBinarno stablo ili binarno drvo usmjereno stablo u kojemu za svaki vrh postoje najviše dva brida kojima je taj vrh početna točka. Katkad se podrazumijeva da je binarno stablo ravninsko.[4] Poseban je slučaj stabla u kojem svaki čvor ima najviše dvoje djece, koja se zovu lijevo dijete i desno dijete. Svaki čvor osim korijena ima točno jednog roditelja, a korijen nema nijednog roditelja.[3] Listovi su čvorovi koji nemaju nijedno dijete.
Potpuno binarno stablo je binarno stablo u kojem su svi listovi jednake dubine, a svi ostali čvorovi imaju točno dvoje djece.
Vidi još
urediLiteratura
urediIzvori
uredi- ↑ a b Teorija grafova i logistika, Hrvatski matematički elektronički časopis
- ↑ a b c Sveučilište u Zagrebu, Geodetski fakultet, Zavod za kartografiju i fotogrametriju Arhivirana inačica izvorne stranice od 19. kolovoza 2019. (Wayback Machine) Nada Vučetić: OSNOVE GEOINFORMATIKE: Neki pojmovi i definicije iz teorije grafova, Osnove teorije skupova (pristupljeno 8. siječnja 2020.)
- ↑ a b Stabla, Hrvatski Wiki o Programiranju. Inačica izvorne stranice arhivirana 14. prosinca 2018. Pristupljeno 6. lipnja 2016.
- ↑ Binarno stablo, Hrvatsko strukovno nazivlje