Superpozicija titranja
Superpozicija titranja različitih frekvencija ili zbrajanje titranja različitih frekvencija je titranje koje nastaje kad na isto sredstvo djeluju dva uzroka titranja različitih frekvencija.[1]




Objašnjenje
urediOsnovna razlika između struje korpuskula (čestica) i valnog širenja pojavljuje se u interferenciji valova. Interferencija dolazi najjasnije do izražaja u činjenici da se dva vala mogu međusobno poništiti. Pustimo li dva vala iste valne duljine i jakosti u jednom te istom smjeru, možemo opaziti, da se valovi neki put pojačaju, neki put oslabljuju, a katkad i potpuno gase. Te su pojave bile od velike važnosti u povijesti optike kao razvidan dokaz da svjetlost nije struja čestica.
Ravne valove prikazujemo harmoničnim funkcijama, kosinusima i sinusima. Neka nam u znači komponentu električnog polja, pomak žice i zgušćaj zraka:
Valna funkcija prikazuje titranje, koje se s konstantnom brzinom širi u smjeru osi x. Valna funkcija ima konstantnu vrijednost, kad je t - x/f = konstantno ili x = f∙t + konst. To znači jednoliko gibanje po osi x. Pri tom valna funkcija može značiti longitudinalni ili transverzalni pomak. S obzirom na to da je f = t∙λ, možemo valnu funkciju pisati u obliku:
Najvažnije svojstvo valnih gibanja očituje se u interferentnim pojavama. Interferencija se osniva na slaganju valova. Složeno valno gibanje može se sastaviti od velikog, pa i beskonačnog broja jednostavnih harmoničnih valova:
Već prema tome, kako se odaberu amplitude i fazne razlike, dobivaju se različite valne funkcije. Strogo matematički može se pokazati, da se svako valno gibanje dade prikazati sumom.
Titranje žice
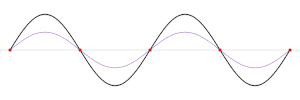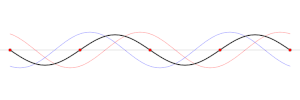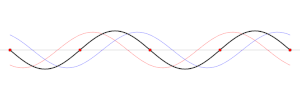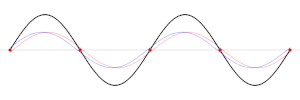
urediNapeta žica titra uvijek tako, da su njeni krajevi nepomične točke. Najjednostavniji stojni val izgleda kao brijeg ili dol razapet između krajnjih točaka žice. Kod takva vala sve točke istodobno titraju prema gore, odnosno prema dolje, i postižu sve istodobno svoje najveće transverzalne pomake iz položaja ravnoteže. Drugi jednostavni stojni val je titranje žice, kod kojeg postoji još jedna nepomična točka u sredini žice. U tom slučaju jedna polovina žice titra u suprotnom smjeru od druge polovine. Jednostavne valove predstavljaju i titranja kod kojih ima više nepomičnih točaka između krajeva žice. Sva ta titranja posjeduju pravilnu valnu krivulju, pa se kod njih može govoriti o određenim valnim duljinama. U prvom slučaju na slici čitava žica predočuje samo polovinu valne duljine. U drugom slučaju žica predočuje jednu potpunu valnu duljinu. Duljinu žice označit ćemo slovom d, a povoljni cijeli broj slovom n. Jednostavni odnos da se između krajeva žice nalazi cijeli broj bregova ili dolova možemo izraziti matematički:
gdje je n = 1, 2, 3, 4, …. Ovim određenim vrijednostima valne duljine odgovara i određeni raspon frekvencija:
Najmanju frekvenciju titranja ima val koji kao jedini brijeg, a zatim dol titra između krajeva žice. Na slici valovi imaju redom dvaput, pa triput veće frekvencije od prvog vala.
Pravilni val s najmanjom frekvencijom zove se osnovni harmonični titraj. Ostali pravilni valovi, koji imaju frekvencije dvaput, triput, i tako dalje veće od osnovnog harmoničnog titranja zovu se gornji harmonični titraji, i to redom prvi gornji harmonični titraj, drugi harmonični titraj, i tako dalje. Osnovna frekvencija f0 je određena prirodom pričvršćene žice.
Zasto smo uveli ova harmonična titranja žice? Odgovor na ovo pitanje daje jedan od najdubljih zakona fizike. Već je D. Bernoulli oko 1750. opazio da se slaganjem pravilnih harmoničnih titranja može dobiti vrlo složeno titranje žice. Pri tome slaganju treba zamisliti, da se pomaci pojedinih harmoničnih titranja zbrajaju ako imaju jednaki smjer ili odbijaju ako su protivnog smjera.
Na slici je prikazano titranje žice koje je nastalo slaganjem iz osnovnog i prva dva gornja harmonična titranja žice. Ova 3 harmonična vala ne titraju istom jačinom; maksimalni pomaci su kod osnovnog titranja veći nego kod gornjih harmoničnih titranja. Stvarno titranje žice pokazuje odstupanje od pravilnih valnih krivulja, koje su tipične za harmonična titranja. Slaganjem pravilnih harmoničnih valova može se dobiti nepravilan val. Na osnovu Fourieriva teorema može se dokazati, da se svako titranje napete žice može dobiti slaganjem harmoničnih stojnih valova. Treba pomisliti da žica istobno izvodi osnovno i sva gornja harmonična titranja. Pomaci pojedinih harmoničnih titranja zbrajaju se ili odbijaju, a taj cjelokupni zbroj u svakoj točki žice ostvaruje se kao njen stvarni pomak. Za svaki pojedini harmonični titraj može se amplituda proizvoljno odabrati. Od jakosti tih pojedinih harmoničnih titranja zavisi, kakav izgled ima promatrano titranje žice. I obratno, iz opažanog titranja žice može se zaključiti, kojom su jakošću zastupana pojedina harmonična titranja.
Interferencije valova nemaju analogije pri kretanju čestica (korpuskula), pa su takve interferentne slike najbolji znak da se radi o valnom gibanju. Samo u valnoj teoriji mogu se objasniti pojave da svjetlost svjetlost daje tamu, a zvuk plus zvuk tišinu. U interferenciji očituju se unutarnji zakoni valnog širenja, ona su izraz osnovne zakonitosti koja vlada kinematikom valova. Slaganjem pojedinih jednostavnih valova mogu nastati najzamršenije valne pojave, no ti se uvijek mogu razlagati na svoje jednostavne sastavne dijelove. Jedino harmonična titranja (titranja s točno određenom valnom duljinom) opažamo kao čistu boju ili čisti ton. Uistinu sve su pojave u prirodi zamršene, ali se uvijek mogu prikazati kao rezultat slaganja harmoničnih titranja s različitim valnim duljinama i smjerovima. Ako takvi sastavi nisu odviše nepravilni, možemo govoriti o pojedinoj boji ili tonu. Kada se, naprotiv, pri takvom slaganju pojavljuju najrazličitije valne duljine, tada se potpuno gubi karakter pojedinih boja ili tonova. Svatko je mogao primijetiti osnovnu razliku između čistog tona kojeg muzičkog glazbala i šuma. Šumovi nastaju ako zvuk vrlo nepravilno pobudimo, na primjer struganjem cipele po podu. Kod ovakvog šuma ne može se govoriti o nekoj jedinstvenoj frekvenciji ili valnoj duljini. Šum se može uvijek rastaviti na mnogo ravnih valova s najrazličitijim valnim duljinama. Šumovi su smjese svih mogućih tonova. Ako brzo na klaviru pobudimo sve tonove, čujemo takve nepravilne šumove. Slaganjem pravilnih valova mogu nastati sasvim nepravilne valne pojave, kod kojih se može potpuno izgubiti svojstvo periodičnosti, koji inače označuju ravne valove.
Ravni valovi sastoje se od valnih fronta koje se rasprostiru po čitavom prostoru kao niz paralelnih ravnina. Prolazom valnih fronta kroz jednu točku, neprekidno se u toj točki periodički ponavlja isto stanje titranja. Takvi ravni valovi dopiru samo tada do nas ako žica pravilno titra bez prestanka. Pravilne tonove čujemo samo kod neprekidnog periodičkog titranja žica ili membrana. Takvi čisti tonovi predstavljaju samo idealizaciju stvarnih fizikalnih odnosa. U prirodi svaki ton ima svoj početak i kraj. Takve tonove možemo prikazati kao rezultat slaganja više pravilnih ravnih valova. U vremenski omeđenim tonovima dolazi uvijek više ravnih valova s raznom valnom duljinom iako samo uski spektar može biti pobuđen sa znatnom jakošću (intenzitetom). Takav je val prosto omeđen, u njemu je sredina nalik na pravilni ravni val, a na krajevima pomalo iščezava. Što je dulji takav val, to čišći je njegov ton. Kada se njegova duljina smanjuje, tada pomalo iščezava karakter tona. Takvi odsječeni tonovi nastaju brzim potezom gudala o violinu.[2]
Izvori
uredi- ↑ "Superpozicija titranja različitih frekvencija", [1] "Institut za hrvatski jezik i jezikoslovlje", www.struna.ihjj.hr, 2019.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.