Gaussov zakon

Gaussov zakon ili Gaussov zakon električnoga polja (po Carlu Friedrichu Gaussu) je fizikalni zakon prema kojemu su silnice električnoga polja otvorene krivulje što izlaze iz pozitivnih električnih naboja, a završavaju u negativnim električnim nabojima, odnosno tok električnoga polja kroz zamišljenu zatvorenu plohu jednak je zbroju svih električnih naboja koji se nalaze unutar te plohe podijeljenome s dielektričnom permitivnošću vakuuma. U integralnom obliku zakon glasi:

Elektromagnetizam

Elektricitet • Magnetizam Elektrostatika Električni naboj • Coulombov zakon • Električno polje • Električni tok • Gaussov zakon • Električni potencijal • Elektrostatska indukcija • Električni dipolni moment • Gustoća polarizacije Magnetostatika Ampèreov zakon • Električna struja • Magnetsko polje • Magnetizacija • Magnetski tok • Biot–Savartov zakon • Magnetski dipolni moment • Gaussov zakon za magnetizam Elektrodinamika Zrakoprazan prostor • Lorentzov zakon • ems • Elektromagnetska indukcija • Faradayev zakon • Lenzov zakon • Struja pomaka • Maxwellove jednadžbe • EM polje • Elektromagnetsko zračenje • Liénard-Wiechertov potencijal • Maxwellov tenzor • Vrtložne struje Električna mreža Električna vodljivost • Električni otpor • Električni kapacitet • Električni induktivitet • Impedancija • Rezonantne šupljine • Vodiči valova Kovarijantna formulacija Elektromagnetski tenzor • EM Stres-energijski tenzor • Četvero-struja • Elektromagnetski četvero-potencijal Znanstvenici Ampère • Coulomb • Faraday • Gauss • Heaviside • Henry • Hertz • Lorentz • Maxwell • Tesla • Volta • Weber • Ørsted

Prikaz električnog polja koje okružuje pozitivni (crveno) i negativni (plavo) električni naboj.

Prikaz električnog polja između dva točkasta električna naboja.

Sferna ljuska predstavlja jednu od "valjanih" Gaussovih ploha.

Polarizirani dielektrični materijal.

Radijalno (poprečno) električno polje pozitivne kugle.

Električni tok kroz cilindričnu površinu.

Električni tok točkastog naboja unutar kugle.

Na rubu kugle, gdje je r jednako R, podudara se električno polje s Coulombovim poljem, što bi ga proizveo točkasti naboj e u centru kugle. Polje u unutrašnjosti kugle neprekidno se nadovezuje na polje izvan kugle.

$\Phi _{E}={\frac {Q}{\varepsilon _{0}}}$

gdje je: Φ_E - tok električnog polja, Q - električni naboj, ε₀ - dielektrična konstanta vakuuma. Tok se nadalje može povezati s električnim poljem:

$\Phi _{E}=\int _{s}E\cdot dA$

gdje je: E - vektor električnog polja, a dA - element površine plohe S po kojoj se integrira. Tok električnoga polja kroz proizvoljnu zatvorenu plohu koja ne sadrži električni naboj jednak je nuli, to jest električni naboj izvor je električnoga polja. Zakon smatramo jednim od četiri Maxwellove jednadžbe.

Iskaz Gaussovog zakona

Gaussov zakon glasi: "Ukupni električni tok kroz zatvorenu plohu je proporcionalan ukupnom naboju sadržanom unutar te plohe." Možemo ga koristiti u integralnom i diferencijalnom obliku.

Integralni oblik Gaussovog zakona

U integralnom obliku zakon glasi:

$\Phi _{E}={\frac {Q}{\varepsilon _{0}}}$

gdje je: Φ_E - tok električnog polja, Q - električni naboj, ε₀ - dielektrična konstanta vakuuma.

Tok se nadalje može povezati s električnim poljem:

$\Phi _{E}=\int _{s}E\cdot dA$

gdje je: E - vektor električnog polja, a dA - element površine plohe S po kojoj se integrira.

Diferencijalni oblik Gaussovog zakona

U diferencijalnom obliku zakon glasi:

$\nabla \cdot E={\frac {\rho }{\varepsilon _{0}}}$

gdje je: $\nabla$ - Hamiltonov operator nabla, ρ - volumna raspodjela naboja, ε₀ - dielektrična konstanta vakuuma.

Oba iskaza zakona su ekvivalentna (jednakovrijedna) jer se temelje na teoremu o divergenciji koji se još naziva Gaussov teorem. Primjenjujući ove oblike zakona mogu se računati polja pravilnih raspodjela naboja (primjerice žice, kugle i slično) ako je dana raspodjela naboja, ili izračunavati raspodjela naboja iz zadanog polja.

Objašnjenje

Jakost električnoga polja opada obrnuto proporcionalno kvadratu udaljenosti od električnog naboja. Na taj isti matematički zakon dolazimo ako usporedimo električna polja sa strujanjem vode. Uzmimo da voda ima izvore tamo gdje se nalaze pozitivni električni naboji, a uvire tamo gdje stoje negativni naboji. Uzmimo dalje da iz svakog izvora istječe u sekundi konstantna količina vode. Kakva će biti brzina vode oko jednog izvora? Voda izlazi iz izvora i struji jednoliko na sve strane u prostor. Zamislimo koncentrične kugle oko tog izvora. Voda prolazi kroz površine tih kugala, a njena brzina ima smjer radijvektora. Očito je da kroz površinu svake kugle prođe ista količina vode. Voda se znatno ne može niti stisnuti niti rastegnuti, pa sve što iziđe iz izvora, proteče kroz sve kugle. Količina tekućine koja prođe kroz površinu jedne kugle može se lako proračunati. Kroz svaki m² kugline površine prođe u sekundi stupac vode koji ima bazu 1 m², a visinu jednaku brzini v vode. Ukupna količina vode koja protječe kuglinom površinom jednaka je dakle umnošku površine i brzine. A to je za nestlačivu tekućinu konstantno:

$4\cdot r^{2}\cdot \pi \cdot v={\mbox{konstantno}}$

Odatle se vidi da brzina strujanja opada kao 1/r². Taj isti matematički zakon vrijedi i za električno polje. Time što ćemo zamišljena električna polja usporediti sa zornim mehaničkim modelima, lakše ćemo naći mnoge zakone. Zamislimo također kuglu oko električnog naboja. Tada možemo opet jakost polja na toj kugli pomnožiti površinom kugle. Dobivamo:

$E\cdot 4\cdot \pi \cdot r^{2}={\frac {e}{r^{2}}}\cdot 4\cdot \pi \cdot r^{2}=4\cdot \pi \cdot e$

Ukupan tok polja kroz kuglinu površinu, dakle, ne ovisi o polumjeru kugle. Kroz sve koncentrične kugle oko naboja prolazi isti tok polja. Ovaj teorem možemo odmah poopćiti. Ako sagradimo plohu od samih dijelova koncentričnih kugli i zraka koje izlazi iz naboja, tad je tok polja kroz tu plohu opet 4∙π∙e. Dio kružnice možemo zamijeniti linijskim dijelom, koji stoji koso na zraku i spaja dijelove dviju koncentričnih kružnica. Općenito se vidi da je infinitezimalni dio kugline plohe jednak kosom plošnom elementu, pomnoženom kosinusom kuta između zrake i normale na kosi plošni dio. Mjesto da množimo plošni dio kosinusom, množit ćemo električno polje E. Tad dobivamo E_n, komponentu polja u smjeru normale (okomice) na plošni dio. Odatle vidimo da je tok polja kroz bilo kakvu plohu koja zatvara naboj konstantan i jednak toku polja kroz koncentrične kugle:

$\int \int E_{n}\cdot {\mbox{d}}f=4\cdot \pi \cdot e$

Usporedimo li polje s brzinom vode, tad nam E_n∙df predočuje količinu vode koja u sekundi proteče kroz površinu df. Važna je samo komponenta brzine, koja stoji okomito na površinski dio df. Samo zbog te komponente protječe voda kroz površinski dio. Gornju jednadžbu možemo čitati tako, da je ukupni tok polja kroz zatvorenu plohu dan jakošću izvora. Sasvim u duhu Faradaya shvaćamo pri tom električne naboje kao izvore i ponore "toka polja".

Integralna jednadžba vrijedi i onda ako ploha zatvara više električnih naboja, ali tada u jednadžbu treba uvrstiti ukupni električni naboj. Ako u plohi nema električnog naboja, tada ukupni tok polja kroz zatvorenu plohu iščezava.

Dosadašnji izvodi vrijede bez obzira na to kako zamišljamo električne naboje. Oni mogu biti pojedine točke ili neprekinute raspodjele. Jasno je da su elektroni i protoni koncentrirani u mala prostorna područja. No o tome da li su to prave "točke" ili "oblačci", nismo dosad mogli ništa reći. Sada ćemo promatrati neprekinuto (kontinuirano) raspodijeljene električne naboje. Tu sliku nećemo toliko primijeniti na sam elektron, koliko na mnoštvo elektrona i iona. Ovdje dakle zaboravljamo na atomsku strukturu elektriciteta.

Iz teorema o toku polja kroz zatvorenu plohu izračunat ćemo najprije električno polje oko jedne beskrajne ploče, koja je jednoliko nabijena električnim nabojem. Iz same simetrije problema proizlazi da električne silnice moraju biti zrake koje, ako je naboj pozitivan, okomito izlaze iz ploče, ili, ako je naboj negativan, okomito ulaze u ploču. Zatvorimo kvadratni metar ploče kockom tako da električno polje izlazi na obje strane okomito na kocku. Ukupan tok polja kroz plohu kocke jednak je 4∙π∙ω, ako je ω električni naboj po 1 m² (gustoća električnoga naboja). Kroz jednu i drugu stranu kocke prolazi jednaki tok polja jednak E∙1 m². Dakle ukupan tok polja je 2∙E∙1 m², a to mora dalje biti jednako 4∙π∙ω. Dobivamo da u okolini beskrajne homogeno nabijene ploče električno polje ima konstantan iznos:

$E=2\cdot \pi \cdot \omega$

Ako usporedo postavimo dvije suprotno nabijene ploče, tada se električno polje između ploča zbraja, a izvan njih poništava. Uzmemo li konačne ploče, dobivamo električni kondenzator. Poznato je da je kod kondenzatora električno polje znatno samo između ploča. Električno polje u kondenzatoru mogli bismo opet iznova proračunati ako promatramo tok polja kroz plohu koja zatvara jednu ploču kondenzatora. Zatvoreni naboj ploče neka je jednak e. Električno polje je od nule različito samo između ploča. Dakle je ukupni tok polja kroz tu plohu jednak E∙f, gdje je f površina kondenzatora. To dalje mora biti jednako 4∙π∙e:

$E\cdot f=4\cdot \pi \cdot e$

Omjer e/f jednak je plošnoj gustoći naboja, pa za električno polje dobivamo:

$E=4\cdot \pi \cdot \omega$

Električno polje kondenzatora je sukladno (proporcionalno) naboju po 1 m². Taj vrlo jednostavan i važan odnos može se primijeniti i na druga nabijena metalna tijela. Iz površine metalnog tijela izlazi električno polje koje je jednako površinskoj gustoći naboja pomnoženoj s 4∙π.

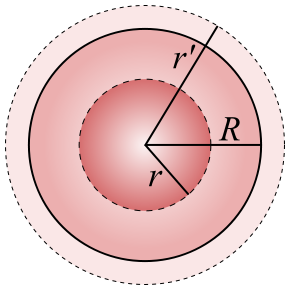
Na osnovu zakonu o toku polja izračunat ćemo električno polje još u jednom važnom slučaju, koji je često poslužio kao model elektrona. Uzet ćemo, da električni naboj jednoliko ispunjava jednu kuglu. Polje izvan kugle slaže se s Coulombovim poljem točkastog naboja, koji bi se nalazio u središtu kugle, a bio bi jednak cjelokupnom naboju kugle. Pitanje je, koliko je polje u samoj kugli, ispunjenoj električnim nabojem. Gustoću naboja u kugli označit ćemo s ρ. Očito je, da električno polje ima smjer radijvektora. Zamislimo jednu kuglu, koja koncentrično leži u uzetoj kugli. Naboj u toj zamišljenoj manjoj kugli jednak je umnošku obujma i električne gustoće. Ukupni tok polja kroz svaku koncentričnu kuglu jednak je okruženom naboju, pomnoženom s 4∙π:

$E\cdot 4\cdot \pi \cdot r^{2}=4\cdot \pi \cdot {\frac {4\cdot \pi }{3}}\cdot r^{3}\cdot \rho$

Za električno polje dobivamo odatle vrijednost:

$E={\frac {4\cdot \pi }{3}}\cdot r\cdot \rho$

Električno polje raste od središta nabijene kugle s udaljenošću r. U središtu kugle polje iščezava. Polumjer kugle označit ćemo s R. Gustoća je jednaka omjeru između ukupnog naboja e i obujma kugle (4/3∙π)∙R^3. Uvrstimo to u gornju jednadžbu i pišemo je vektorski:

$E={\frac {4\cdot \pi }{3}}\cdot r\cdot \rho ={\frac {e}{R^{3}}}\cdot r$

Na rubu kugle, gdje je r jednako R, podudara se električno polje s Coulombovim poljem, što bi ga proizveo točkasti naboj e u centru kugle. Polje u unutrašnjosti kugle neprekidno se nadovezuje na polje izvan kugle. Zamislimo jednu koncentričnu kuglinu plohu oko kugle naboja. Tok polja kroz tu plohu očito ne zavisi od toga da li je naboj unutra raspodijeljen u većoj ili manjoj kugli, ili čak stisnut u jednu točku. Odatle se jasno vidi da se polje izvan nabijene kugle podudara s poljem točkastog naboja. Pokusima je dobro ispitano samo električno polje u priličnoj udaljenosti od elektrona. Na osnovu toga ne možemo zaključiti, da li je elektron "točka", obdarena masom i nabojem, ili je oblak elektriciteta.

Iz našeg izvoda vidimo da je električno polje u nekoj točki u kugli prouzrokovano samo onim električnim nabojem koji leži bliže središtu nego ta točka. Odatle možemo zaključiti da električno polje u unutrašnjosti nabijene kugline plohe iščezava. To je poznata iskustvena činjenica. Ona služi kao vrlo točan dokaz Coulombova zakona.

Pretpostavka da je električni naboj neprekinuto (kontinuirano) raspodijeljen vodi do toga da električno polje ne postaje beskonačno. U središtu kontinuirano shvaćenog elektrona polje iščezava. Ovdje vidimo drugo značenje gustoće naboja. Kontinuirana raspodjela naboja uklanja singularitete električnog polja (beskonačno velike gustoće).

Vanjske poveznice

• Odgovori na ispitna pitanja prema predavanjima iz elektromagnetizma prof. Emila Babića  Arhivirana inačica izvorne stranice od 24. prosinca 2012. (Wayback Machine)